Looking for the trending summer nail designs of 2024? With over 100 options, these summer nails are sure to be a hit!
The summer is the one time that I almost always have my nails done. When you’re in a super cute swimsuit at the beach with a straw hat and rocking a nice tan, gorgeous summer nails really complete the look.
The great thing about doing your nails is that you can try out fun seasonal summer nail designs! And this summer, there are some really cool looks.
Nail trends don’t change a ton from year to year, but there are crucial small differences. A few years ago, stark white nails were not in; last year, white was the color over 85% of women were wearing during the warmer months.
This year has some of the coolest summer nail trends yet!
Major Summer Nails Trends:
This summer, the trends are very similar to last, but there’s an emphasis on art. In 2023, various interesting summer nail designs are still “in,” but they’re all slightly abstract and upscale. Focus on adding just a touch of summer through color, pattern, and design.
As far as the shape goes, almond and square are both popular this year. If your nails are short, I recommend asking for gel tips with a dip manicure. I find that the dip manicure works best because it keeps your nail strong so it doesn’t break.
Don’t forget: if you opt for press-on nails, you can always cut and file them yourself to fit the current nail shape trend. I like to buy press-on nails on Etsy, but I use this glue to get them to stick for a good long while.
Shiny nails seem to be much more popular than matte this year.
Specific summer nail designs that are popular this year include:
- Abstract summer nail designs in one color (use different shades of the color to achieve a seamless look)
- Floral designs in beachy summer nail colors
- French tips covered with summer nail designs
- Rainbow nails
You’ll see that a lot of color is popular this year as you scroll through the summer nails photos below. You have a choice between staying on one side of the color wheel (which means you use various shades of similar colors, like red/orange/yellow or blue/greens), or using opposite summer nail colors (i.e. red with blue). While staying on one side of the color wheel seems to be more popular this year for summer manicures, you’ll definitely find both options here.
Summer Nails Inspiration
Here are 100+ gorgeous summer nails for 2024! Some of these are pretty complicated summer nail designs while others are simple summer nail colors.
Feel free to save any of these photos to your phone so that you can show your nail technician. Just press down on the photo and click save to camera roll.
Blue nails in the summer truly remind me of beaches and beautiful oceans. And these particular summer nails are just the perfect design for blue summer nail colors! The wavy patterns on each accent nail just make me think of beach waves and the sound of the ocean as you go for a stroll around the shore.
For bold pops of color that won’t be too overwhelming on the eyes, try polka dot patterns on top of a classic French manicure. Use a mixture of bright oranges and soft pinks for every dot to recreate this fun, summery manicure!
If you’re unsure of what kind of summer nails to do next, you can always try florals. It’s a simple design that’s wearable every day. Opt for dainty flower patterns for a more feminine vibe. As for summer nail colors, I suggest picking bright shades like yellow, blue, and red, especially during the summer season!
I love matte finishes on a manicure. They just look so chic and they’re such a refreshing change of pace from the usual satin or glossy finish. But apart from that, this particular manicure just really catches your eye with an interesting mix of orange and blue summer nail colors atop a nude base coat. The dainty swirl patterns give it a more unique touch too!
I can totally see shades of orange being popular this summer. And what’s not to love? Orange summer nail colors just really remind me of beautiful sunsets as you take a stroll on the beach. If you’re in doubt, just take a look at this pretty, orange floral nail art! These are definitely some of the top trending summer nail designs right now.
Green is an ideal summer color too! But it’s also a versatile color that can fit almost any season all year long. I suggest opting for a sage green shade for a chicer and more sophisticated look on your nails. These summer nail designs are simple but chic and are trending this year.
I usually reserve pastel shades for the spring, but they also look great as summer nail colors too! They give your nails this soft and feminine touch that’s ideal for daily wear. If you’re not into bold and bright colors, go pastel!
Looking for summer nails that work on shorter nails? Try adding in a floral design.
I just love this shade of green! They’re so pretty and you can pair them with different variations of floral patterns. But on this particular manicure, daisy nail art is totally perfect!
If you’re feeling fruity this summer or simply want to take a break from your usual French tips or floral patterns, why not try these lemon-themed summer nail ideas? The yellow summer nail colors would be so ideal as the weather gets warmer. And in the summer, your nails will feel so refreshed with this nail design!
Pink is another of my go-to summer nail colors. They’re just so effortlessly feminine, flirty, and versatile! You can play around with pink as much as you when it comes to nail art and these swirly patterns with white accents are just one of them!
Can’t decide on a single nail art for the summer? Why not pick a different pattern or design for each of your nails just like in the photo? This would look so cute and quirky and totally unique! You can either opt for summery elements to match the theme or pick summer nail designs that you like.
I love the daintiness of these particular summer nails! The blend of white and a little bit of silver looks so chic and sophisticated. White nails just give off such an effortlessly classy vibe that you can wear them all throughout summer or all year long. Whether you want them casual or for formal occasions and events, you can never go wrong with white!
Here’s another set of swirly patterns for summer! But this time, you’ll be playing with orange, purple, and white summer nail colors for that beautiful pop of color! The use of negative space around the nail art makes this not too overwhelming for the eyes as well.
These minty floral nails are utterly pretty! You can never really go wrong with a floral design. They just go well with everything and are also pretty easy to do even if you’re just a newbie when doing your own nail art.
Here’s another set of white and silver summer nails that’s perfect if you’re looking for something dainty and minimalistic! It’s just enough of a twist to make your classic French tips not look too traditional. These would look so good with pearl jewelry and accessories.
This combination of blue and purple looks so cute! It gives me serious mermaid and underwater vibes! The swirly patterns on the nail accents remind me of the look of iridescent beach waves.
If you’re looking for a simple green manicure that you can do comfortably at home without too much fuss, this one’s for you! Pick a softer shade of green like sage or olive for a much chicer look!
I love how quirky and fun these summer nails are! From the combination of bold, bright summer nail colors to the mix of different patterns to create this unique look is just utterly gorgeous! It’s a blend of abstract art that’s so perfect for the summer season.
Sometimes all you really need are flowers. Keep your base coat bare or colorless then top it off with florals of different summer nail colors. These are pretty easy to do as well! All you need is a metal nail dotter to recreate each flower on your nails.
I love the colors used on these nails! They’re so ideal for summer and I love how this manicure almost reminds me of abstract paintings in museums.
Want something a lot more minimalistic and not too eye-catching? Try this manicure out! It’s dainty, it’s easy to DIY, and it’s classy too! You can go for the same shades of green as in the photo or pick the colors that you prefer.
One way to subtly spice up a classic French manicure is by using different summery colors for each painted tip. Forego the usual whites and pick beautiful, bright colors for the summer! You can even opt for the same color but in different shades and tones for a gradient effect.
There’s something about these dainty and wavy summer nail designs that reminds me of the beach. And now, I’m suddenly missing the feel of the ocean on my skin. But in the meantime, I will settle for these gorgeous nails.
Mix and match trendy wavy patterns with florals for a unique and interesting summer manicure. Personally, I am obsessed with the combination of oranges and pinks on these summer nails. Definitely one of my favorite color combinations this year.
If you don’t want nails that are too bold and bright, pink pastel shades for your French manicure this summer season. Top it off with dainty daisy nail art and you’ll be all set!
Aside from switching up the colors of your French tips, another way to spruce up this classic manicure is by topping it off with dainty floral summer nail designs! Pick summery colors to match the season or simply pick your favorite polish colors!
Here’s another variation of the floral French manicure on this list. This one puts the florals just right around the tips and none on the base of the nails. This gives a slightly more minimalistic look and puts the attention all on the tips of your nails.
Here’s one of my favorite summer nails on this list. I just love the combination of purple, greens, and blues. So perfect for my kind of summer! Pick a different nail art pattern for each nail to get this unique look!
Teal or a mint green color is so perfect for the summer! As the weather gets warmer, I’m sure a lot of us are in need of something refreshing. While we can sip our favorite drinks, our nails can still look just as cool and fresh with these colors.
So classy and sophisticated, these muted green nails with wavy nail art are utterly gorgeous! They look sleek and chic and utterly fabulous! If you like a more understated manicure for the summer, this is a must-try.
I love this shade of baby blue nails! They look so pretty and just as ideal for the summer season. As much as I love bright and bold colors that will catch everyone’s eyes, these soft pastel shades are so gorgeous that I can’t help wanting them too.
But if soft, muted colors are not your thing, then you’re sure to love these bold pink and oranges for your summer nails. Pair them with some dainty florals and popular patterns like these waves for a fun, summery manicure.
If you want something simpler to do that you can recreate at home, these bright orange French tips are for you! You can either opt for the same shade of orange or pick another summery color.
I am loving these neon nail art designs for the summer! They’d be so perfect to wear on a beach or pool party with friends. Your nails will surely make a splash!
If you’re not too fond of doing intricate nail art for your summer manicure, then why not go for the classic route? Do a simple coat on your nails but give it a little twist by using different summer colors for each nail.
This asymmetric French tip looks so cool and modern! Give it a summer twist by using bright colors against a nude base coat.
If you feel like white nails might be a little too plain for you, you should definitely give this particular summer nail design a try! It’s a lot more interesting than your usual French tips.
But if you can’t let go of your go-to French manicure, then why not spice it up by doing gradient colors? Pick out different shades of green or blue to give it that gorgeous gradient effect.
If you’re looking for ways to freshen up the traditional French tip, try this asymmetrical design! Top it off with a darker shade of the color you chose for more dimension on your manicure.
Yellow is one of my favorite colors to wear for the summer, and this particular nail design is utterly pretty! Ask for a square cut shape for your nails to recreate these patterns.
There’s something so beautiful about using soft gel for your nails. The clean, transparent look along with those orange wavy patterns gives such a classy and sophisticated look that’s perfect for any summer holiday.
Spice up a monochrome manicure by doing French tips and reverse French tips using the same color in different shades. Pick a lighter and a darker shade to place on the tips and the base of your nails.
If you want the color of the ocean on your nails, this beautiful bright teal is for you! Recreate wavy patterns for your accent nails to get that beachy feel.
This shade of green is so cute! Mix your classic French tips with a simple monochrome manicure if you want a pretty straightforward and easy-to-do summer nail.
I am totally obsessed with these seashell-themed nails! It definitely makes me miss the beach more, but I cannot think of a more suitable nail to satiate my excitement for the summer season.
If you feel white nails might be a little bit basic for the summer, try to spice it up by painting your accent nails with these gorgeous gradient colors!
Here’s an interesting way to do color blocking on your summer manicure. Along with the gorgeous combination of pink and purple, you can either opt for a nude base coat or a completely transparent one!
If you find orange a little too bright and bold, you can opt for this shade instead. It’s pastel, it’s softer and more muted.
Here’s another favorite of mine on this list. Apart from the bright, summer colors, I love the abstract, wavy patterns on these square-shaped nails!
Almond nails are a classic for a reason and what better way to paint them than an asymmetric French manicure? To make it even more interesting, use two colors for your tips!
I love the gradient effect on these nails! The pinkish tips give this manicure such a nice flush of color. And the dainty gold linings really just make this manicure pop!
These white marbled nails with gold foil detailings are absolutely gorgeous. I’d reckon they would fit the winter season too!
I’m loving these florals atop a matte base coat. It has such a gorgeous, vintage feel to them and I love how detailed and dainty they look!
Add a touch of sparkle to your nails with some accent glitter polish in between bright, summery colors on your manicure.
Express those summer vibes by doing tropical leaves for your accent nails! Using black polish against bright pink nails would be so cute!
These orange and yellow nail art with daisies are the epitome of summer to me! From the bright colors to the dainty florals, it’s absolutely gorgeous!
This summery color combination reminds me of the groovy 70s so much! And those smiling daisies are so adorable too!
This particular nail design might be a little icy for the summer but I do think it fits perfectly well for the warmer season!
I love the combination of florals and polka dots in these nails! And if you find applying nail polish and doing nail art a little too fussy for you, you can always opt for nail stickers to do the trick for you!
If you’re looking for a summer manicure that looks luxe, glam, and sophisticated, these nails are for you! I love the dainty linework of glitter to give your nails some sparkle.
Green might not be your first choice when painting flowers on your nails, but these look utterly gorgeous! Opt for a longer cut of nails for a more feminine look.
These nails look so refreshing to look at! Fruity summer nail designs are so cute and quirky and these watermelon-themed nails are so much fun.
White nails really do make your manicure look effortlessly classy. The sharper-shaped nails look so well with it too!
If you want a more unique set of summer nails, this abstract nail art would be perfect! The varying patterns on each nail make the whole look so interesting.
A colorful French manicure is great on its own, but if you want to give it a little oomph, try placing a dainty, little dot on the base of your nails.
But if you don’t feel like putting dots on your nails, go for the classic route and just do a colorful French manicure that’s perfect for summer.
I love this shade of blue so much! It reminds me of clear, sunny skies in the summer but it’s just at the end of your fingertips.
I love this transparent set of nails with dainty, wavy linework. You can use different colors for each hand or go monochrome.
Here’s another way to spice up a classic French manicure this summer season. Pick one accent nail to fully coat with the nail polish of your choice.
I love this combination of blue and white. It looks so classy, elegant, and sophisticated. The nail art also gives a fresh feel to your nails during the summer.
These particular summer nails remind me of the coastal grandmother aesthetic for some reason. It so classy and chic.
A white and nude base coat is just so effortlessly sophisticated. Just look at these nails! You can wear them all summer long and it’ll fit any occasion or event.
Here’s another white and nude manicure that’s as sophisticated as the last one. The dainty linework on this one gives it a much more minimalistic feel that looks sleek and chic.
These pastel squiggles with white detailing are so cute and perfect for the summer season! You can even go for different shapes and sizes for each pattern.
If you liked the dainty white linework from the previous manicures, here’s one that has an almond-shaped cut for those who aren’t too fond of square cuts.
I love this under-the-sea-themed manicure for the summer season! This makes me miss swimming at the beach even more now.
Here’s a cool twist to the usual French manicure. Instead of a basic white tip, you can go for squiggly lines with a combination of summery colors like different shades of orange.
If you want something brighter than orange for your summer nails, go for yellow! It’s bright, bold, vibrant, and everything we love about the summer season!
But if yellow or orange might be a little too bright for your liking, a nice, calming blue might just be perfect for your nails.
I love the look of these rainbow nails! They look so colorful and fun and just so ideal for the summer season. Save those deep, moody colors for the winter and fall seasons.
This shade of blue is so perfect for the summer! I can totally see this being worn during pool parties.
Here’s another blue-colored summer manicure that you can wear on your next pool party or any summer vacation or holiday!
Can’t get enough of this shade of blue? Here’s a design that you might like as well! It has two nail accents with white linework for a dainty touch.
Pink and green are certainly one of my favorite color combinations for the summer. Use them in these abstract squiggly patterns with soft gel nails for a pretty summer manicure!
If you want something simple and girly for the summer, you’ll want to try out this pretty straightforward manicure!
I am just in love with these pearlescent nails! It’s also a gorgeous and elegant way to spice up your classic French mani.
Yellow nails tend to be quite vibrant but this shade of pastel yellow is a bit more muted and soft. It’s perfect if you don’t want a too bright manicure.
Quirky and lots of fun to look at, why not opt to combine two different summer nail designs? This one features smiley faces and cloud-themed nail art.
I’m loving these purple gradient nails! Pick a different shade of purple for each nail to achieve this gorgeous gradient look!
These dainty florals look utterly gorgeous. They look so feminine and soft. I would wear this along with my favorite sundresses during the summer!
Paint some dainty black linework to your summery nails to add more dimension to your manicure. This really makes your nails look so modern!
These pastel patterns are utterly adorable! They kind of almost remind me of those gorgeous lava lamps.
These pastel florals are just as beautiful for the summer season as they are for spring!
Blue nails are one of my favorite manicures to do on my nails. The combination of light and dark blue tones in this one is so pretty!
These graphic nails with minimalistic details and lots of negative space look so chic and modern! It’s a must-try if you want to look trendy this summer!
These sage nails are so understated yet so pretty! I love the half color-half negative space look.
These orange gradient French tips remind me of sunsets during the summer season. It’s utterly beautiful!
Here’s a modern take on color blocking. Use negative space to put a gap between two different colors on your summer nails.
These summery florals look so good atop transparent soft gel nails! The best thing about them is they can easily suit any cut or shape of nails.
These mismatched colored tips look so cute and quirky! Pair them with a nude base coat or maybe even a transparent one.
A classic square-cut nail deserves a classic manicure like these colorful French tips!
When I have a favorite color, I love to wear them on my nails. But with this kind of nail design, I pick the same color in two different shades.
These red and yellow florals on a French manicure are a combination I utterly love! It’s so eye-catching and striking!
These sunny and somewhat earthy-toned colors are to die for! Definitely one of my favorite color combinations on this list.
These orange gradient nails are so gorgeous and ideal for the summer season! Opt for ballerina-shaped nails to achieve this manicure.
Here’s another way you can do a red and yellow color combination. Use them with floral and wavy patterns like in this image!
This asymmetrical French manicure is so cute and unique! It’s a nice way to take a break from the usual French tips.
Here’s another asymmetrical French tip that you can try. But instead of using different colors for each nail, you can just opt to pick one color that you really like.
Here’s one of my favorite summer nails on this list! I’m obsessed with the paint splatter patterns of gorgeous summer colors.
I love this modern take on the classic French manicure! The red and yellow colors against the negative space make them stand out so much!
These strawberries and cream nails are so gorgeous! Your nails would look good enough to eat!
For some fun animal print-themed manicures, go for the trendy cow patterns!
These pastel hearts are so cute and ideal for both summer and spring! If you’re in those months between two seasons, these should be your nails!
I love how feminine these different shades of pink are on the nails! Opt for a longer cut for your nails to keep things even more classy.
Bright blue florals on the nails look so ethereal! Just look at how good this looks!
These swirly, colorful patterns kind of reminds me of melting ice cream for some reason. But they look really unique and interesting as a summer manicure!
For a burst of freshness on your nails this summer season, try out this fun and bright grapefruit-themed manicure!
These nails are utterly adorable! The fruits as nail art kind of remind me of those refreshing drinks you get during the hotter seasons.
At first glance, I would have thought this was better suited for the colder seasons, especially winter. But this kind of blue reminds me of calm ocean waves that are fit for summer too!
If your favorite color’s blue and you like putting glitter around your nails, this is a manicure you’ll love to do!
I love this combination of pink and orange and a little bit of blue! The starry patterns make this look quite ethereal too!
This bright orange manicure is so ideal for the summer! Those tropical flowers are so perfect to wear on a summer getaway.
These melted linework patterns look so chic! I would totally wear this around the city on a warm, summer day.
These pastel squiggly lines remind me of melted popsicles! During the summer, this would look so good on the nails!
Add a pop of glitter to your matte monochrome white nails this summer season to keep things interesting!
If you have had enough of doing florals with glossy finishes, try out this gorgeous matte floral manicure instead! You can never go wrong with daisies!
I love this combination of green and blue on the nails! The melting tips look so chic and modern!
This shade of green is utterly gorgeous! Not only do they look great as a classic French manicure, but you can top them off with some flowers too!
If you want to get colorful this summer season but don’t want it all over your nails, try these rainbow-themed tips instead!
Nothing beats the beauty of a classic marbled nail, and this manicure just proves it. Add some glitter for an extra dash of shine to your nails!
This soft, lilac shade is utterly gorgeous! Use soft gel on your accent nails to top off with beautiful floral summer nail designs.
I love how heavenly and ethereal these cloudy nails look! You can even paint some white sparkles to make them stand out even more!
These artsy, graphic nails are so cool and quirky! It’s good for those who don’t like monochrome summer nail designs.
Impress everyone with this bright teal manicure! Add some tropical nail art to make your nails even more summery!
I love how vibrant and fun these cloud-themed nails are! It’s so summery and bright and it’s a good way to practice your nail art skills too!
These soft-toned tips are so gorgeous! The asymmetrical design gives it a more modern look as well!
I am obsessed with this shade of deep blue! It reminds me of the blue waters of the ocean and it’s such a refreshing sight to see on the nails!
Here’s another shade of blue that you might like. This one’s softer with chunky glitter for extra sparkle and a marbled accent nail.
This shade of baby blue against black makes such a stunning contrast of colors on the nails! Use tropical flowers and some dainty linework for an interesting nail art design.
Here’s another tropical-themed summer nail you might want to try out when the weather gets warmer!
If you love the look of succulents or just want to try something new for your nails this summer, then you should definitely give this a try!
When in doubt, you can never go wrong with a classic, monochrome manicure like this one! Pick a summer color to match the season!
I love the contrast of subtlety and pops of color with this manicure! Keep the tips of your accent nails with a marbled design while the rest of your nails stay natural.
For minimalistic nail art this summer season, give this one a try! It’s a pretty easy nail art that you can practice with at home.
I always say that some of your best accessories are your nails! So why not add a little bling to your manicure to keep them sparkling?
I love the different combinations of summer nail designs on this manicure. Make one of your accent nails that’s just a full, glitter nail and one with abstract nail art while the rest are your usual basic, monochrome manicure.
I love the vintage floral nail art on these nails! Not to mention, this shade of green is utterly stunning and elegant too!
Bright colors like this shade of orange would suit so many skin tones during the summer! They give such a vibrant and bold vibe that’s perfect for the warmer weather.
I’m loving the gradient blue design on these nails! I do think longer nails would suit a gradient design so well to get the full effect!
But if you’re not too fond of having long nails like me, then you might want to check these blue nails out instead! It has geometric patterns that are so modern and chic nowadays.
Pink is such a versatile and fun color to work with. Aside from feminine summer nail designs, you can also paint tropical patterns on your pink nails to get the perfect summer manicure.
If you don’t like a lot of fuss around your nails and want to keep it simple, you can always go for a monochrome orange manicure. Ask for stiletto nails from your manicurist if you’re not fond of short nails.
This one’s a little similar to the previous image, but the nails are in a ballerina-shaped cut.
These gorgeous powder blue nails are so lovely! They look so pleasing to the eye and they’re the perfect base coat for some intricate floral nail art.
If you don’t want to stick with just one color, you can go for different shades or colors for each nail this summer.
I love these floral-themed French tips! They look so feminine, soft, and elegant!
I am loving these quirky, abstract graphic nails! So trendy, modern, and lots of fun to do for the summer season!
Yellow is such a gorgeous color that’s ideal for the summer season so why not give it a try this year? You can even put some floral nail accents for a more feminine and dainty look.
This combination of nude and teal on the nails are so pretty! Add some gold foils and black leaves and you’re all set!
These kinds of manicures just really remind me of a mermaid’s nails. From the pearls and the seashell accents, it’s definitely a nail design I’m going to try out this summer!
If you love these dainty and intricate florals on your nails but can’t do them on your own, you can always go for nail stickers or leave it all to your manicurist to do the job!
These tropical-themed nails are so cute and ideal for summer! I love the neutral color scheme and how it looks quite classy!
These nails are going to make you starry-eyed with this design! The nude base coat makes the overall look sophisticated.
Elegant and sophisticated is what I’d describe these nails! The dainty plant-themed design is so gorgeous and something I’d definitely try out this year.
For a refreshing design, try these citrus fruits as your nail art this summer!
These marbled nails don’t just look glam and luxurious, but they also remind me of beautiful shores around the beach.
A graphic, neon squiggly linework would totally look good during the summer! It’s also a pretty easy nail art to do at home if you don’t feel like going to your nail artist.
Just look how cute these bright blue nails are?! The glittery butterfly accent nail just ties the whole look together!
I’m sure you’ve already seen a lot of wavy linework on this list when it comes to nail art. But this one has a combination of purple and pink that you might want to try out!
This minimalistic and dainty polka-dot manicure looks so trendy and modern! If you want nail art that is subtle and sleek. this one is for you.
If you’re missing the ocean as much as I do, this seashore-themed manicure might just be perfect for you!
Can’t get enough of wavy, squiggly lines on your nails? Maybe you should try out this beautiful blue color combination next!
Give your French manicure a summer twist by using a bright, neon orange as the color of your nail tips.
Add a splash of color to your nude nails with some gorgeous blue-marbled patterns to create gorgeous accents.
I love this shade of mint green. It looks so refreshing on the eyes and the tropical leaves create a nice summery feel.
The color blue is such a perfect shade to do wavy patterns. I think this would look against a transparent base coat for some modern negative space look.
Here’s another French manicure that won’t leave you feeling blue! This baby blue shade is so pretty!
These flowers are so perfect for the summer! Though I do get they can be quite difficult to do for rookie nail artists. But if you want a fuss-free application, you can always opt for nail stickers or press-on nails.
I usually paint my nails brown during the fall season but if it looks this good, I’ll make an exception.
Dainty and easy to do, all you need is a metal dotter to recreate these flowers on your monochrome nails!
I am honestly looking forward to my next beach vacation. But for now, I’ll settle for these gorgeous ocean-themed nails.
Here’s another sea-themed nail you can do for the summer. This one has a white base coat that really makes those blue tones pop!
The contrast between these light and dark blue shades looks so gorgeous! I bet this would look even better with negative space between each pattern.
Mix and match the trendy wavy patterns and basic, monochrome nails this summer season to get some nice dimensions on your manicure!
These blue wavy patterns would look so good on a poolside party this summer season!
Fruit-themed nail art gets so popular during the summer. So what better way to dip your fingernails into something fresh than by painting some fruits like cherries on your nails this summer season?
This dainty French manicure is so pretty and elegant to look at! A thinner line on the tips makes it even more sophisticated.
Create gorgeous contrasts on your nails with these trendy and summery patterns that are perfect for any beach or pool party.
I am obsessed with these kinds of graphic nail art! I just love the neutral color scheme and how unique each nail looks.
If you’re looking for iridescent nails this summer season, this is a nail design you’ll certainly love!
I love how elegant this classy marbled nail art is! It would look so good when you’re wearing formal dresses or going on events!
These abstract nail patterns are so creative and unique! They go so well with bright, neon colors too!
You can never go wrong with pastel colors in the summer season. Put them in wavy patterns and you’ll get this chic manicure!
This is a nice white because it isn’t insanely stark but will still stand out against most skin tones (and work with most outfits).
This is one of my favorite summer nail colors for pale skin! It looks great with any skin color but is especially a good choice for those with skin that doesn’t tan easily.
Put yourself in those summer vibes by adding a tropical tree as an accent nail to your next summer manicure!
You can never go wrong with the classics. These soft, pastel nails are perfect for any occasion and season!
Navy blue is one of the best summer nail colors for pale skin. I love how the navy is slightly preppy so it will never go out of style.
I love the subtle prints in this pastel manicure! It’s perfect for those who don’t want anything too loud or too bold on their nails.
Here’s another simple and plain manicure that you can do in the comfort of your home this summer season!
If you want something a little brighter, go for a pretty yellow shade like this one!
This is one of the prettiest summer nail colors! I love how it’s simple (and neutral) but still has a summer feel. These are stick on nails so they’re easy to use in a pinch.
A monochrome white manicure looks so gorgeous and classy on the nails. It’s a color that can easily suit any style or mood.
Forego your usual French tips and make a statement by adding some accents to the base of your nails instead this summer!
Here’s a monochrome manicure for your summer nails with the subtlest hint of sheen for those who don’t want anything too sparkly.
This bright coral manicure is so ideal for the summer. It reminds me of cocktail drinks and refreshing fruit juices for some reason.
For an icy look this summer to cool you down during the hot weather, this manicure is for you.
Glamorous and luxurious are two words I would describe this summer manicure. If you’re planning on riding a yacht this summer season, this is the manicure to get!
Looking for simple but classic summer nails? The best thing about white nails is how easy they are to accessorize and spruce up!
Make your nails pop with this cute light coral polish for the summer season!
If you really want to make your nails pop, try incorporating rings. I like to do a few on each hand. There’s lots of rings available on Amazon that are pretty decent quality for a low price!
Some hand jewelry will give your nails that extra flair that makes them stand out. Even the prettiest summer nail colors can benefit from some rings calling attention to your hands.
Another important piece to make your summer nails look especially amazing is a nice tan. Whether you’re super pale or naturally tan, you can always add a few levels or even just get a nice glow that makes summer nail colors really stand out.
While nails especially look great with a tan and add an important extra element to any outfit. If you’re not the type that likes to lay out in the sun (and you want to be especially careful with your skin), then opt for a spray-tan or an at-home tanning lotion. Make sure to apply either before you do your nails, especially if they’re a light color!
If you’re looking to do your own get nails at home, head here for my full guide! It’s a quick and easy way to get gorgeous nails all summer long without having to sit and pay at a salon.

































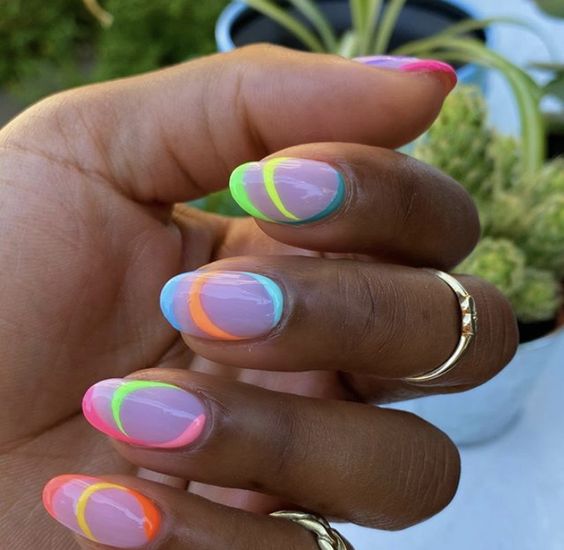


















































































































































































Great article. Turquoise nails are beautiful.